|
| | IProcess (const unsigned &n, const unsigned &num_dims) |
| | The constructor. More...
|
| |
| const Eigen::VectorXd & | GetParameters () |
| | Return the column vector of model parameters. More...
|
| |
| unsigned | GetNumDims () |
| | Return the number of dimensions in the process. More...
|
| |
| void | SetParameters (const Eigen::VectorXd &v) |
| | Set the model parameters. More...
|
| |
| virtual void | NegLoglikelihood (double &objvalue, Eigen::VectorXd &Gradient)=0 |
| | Returns the negative loglikelihood value and the gradient vectors. Given a collection of sequences \(\mathcal{C} = \{\mathcal{S}^c\}\) where \(\mathcal{S}^c = \{t^{c,d}_i\}^{d=1\dotso D}_{i=1\dotso n^c_d}\), and \(n^c_d\) is the number of events on dimension d in sequence \(\mathcal{S}^c\). The negative loglihood of observing \(\mathcal{C}\) is defined as
\begin{align} \ell(\mathcal{C}) = - \sum_{d=1}^D\frac{1}{|\mathcal{C}|}\sum_{c=1}^{|\mathcal{C}|}\Bigg(\sum_{i=1}^{n^c_d}\lambda^*_d(t_i^{c,d}) - \int_{0}^{T_c}\lambda^*_d(\tau)d\tau\Bigg), \end{align}
where \(T_c\) is the observation window of the sequence \(\mathcal{S}^c\). More...
|
| |
| virtual double | Intensity (const double &t, const Sequence &data, Eigen::VectorXd &intensity_dim)=0 |
| | Returns the summation \(\sum_{d=1}^D\lambda^*_d(t)\) of the intensity value \(\lambda^*_d(t)\) of each dimension in a given sequence data at the time t. More...
|
| |
| virtual double | IntensityUpperBound (const double &t, const double &L, const Sequence &data, Eigen::VectorXd &intensity_upper_dim)=0 |
| | Returns the upper bound of the summation of the intensity value on each dimension from time t to t + L given the history of past events in sequence data. Let \({\lambda_d^*(t)}\) be the conditional intensity function on the d-th dimension where \(d=1\dotso D\), and num_dims_ = D. This function returns
\begin{align} \lambda_0^D(t) \geq \sum_{d=1}^D\sup_{\tau\in[t, t + \tau(t)]}\lambda^*_d(\tau), \end{align}
where the returned value \(\lambda_0^D(t)\) will be used for Ogata's Thinning algorithm. More...
|
| |
| virtual double | IntensityIntegral (const double &lower, const double &upper, const Sequence &data)=0 |
| | Returns the integral of the intensity function \(\int_{a}^b\lambda^*(\tau)d\tau\) where \(a = lower\) and \(b = upper\). More...
|
| |
| virtual void | Gradient (const unsigned &k, Eigen::VectorXd &gradient)=0 |
| | Returns the gradient w.r.t. the model parameters on the k-th sequence. More...
|
| |
| void | PlotIntensityFunction (const Sequence &data) |
| | Plots the intensity functions based on the given sequence. It plots the intensity function and the associated event points up of each dimension in the same figure. More...
|
| |
| void | PlotIntensityFunction (const Sequence &data, const unsigned &dim_id) |
| | Plots the intensity function and the associated event points of the dimension dim_id. More...
|
| |
| virtual double | PredictNextEventTime (const Sequence &data, const unsigned &num_simulations)=0 |
| | Predict the next event timing by the expectation \(\int_{t_n}^\infty tf^*(t)dt\). Currently, we use the sample average by simulations to approximate the expectation since the conditional density \(f^*(t)\) normally does not have an analytic form. More...
|
| |
IProcess defines a general interface for each specific point process.
The IProcess class provides the basic interface for a general point process, which can be used for general fitting, simulation, and model checking. Customized point processes are supported by simply inheriting from this class.
Definition at line 20 of file Process.h.
| virtual double IProcess::IntensityUpperBound |
( |
const double & |
t, |
|
|
const double & |
L, |
|
|
const Sequence & |
data, |
|
|
Eigen::VectorXd & |
intensity_upper_dim |
|
) |
| |
|
pure virtual |
Returns the upper bound of the summation of the intensity value on each dimension from time t to t + L given the history of past events in sequence data. Let \({\lambda_d^*(t)}\) be the conditional intensity function on the d-th dimension where \(d=1\dotso D\), and num_dims_ = D. This function returns
\begin{align} \lambda_0^D(t) \geq \sum_{d=1}^D\sup_{\tau\in[t, t + \tau(t)]}\lambda^*_d(\tau), \end{align}
where the returned value \(\lambda_0^D(t)\) will be used for Ogata's Thinning algorithm.
- Parameters
-
| t | the starting time. |
| L | the duration. |
| data | the given sequence of the past events until time t. |
| intensity_upper_dim | a column vector of size num_dims_ storing the upper bound of the intensity function on each dimension from time t to t + L. |
- Returns
- the summation of the upper-bound of each intensity function from the respetive dimension within the interval [t, t + L].
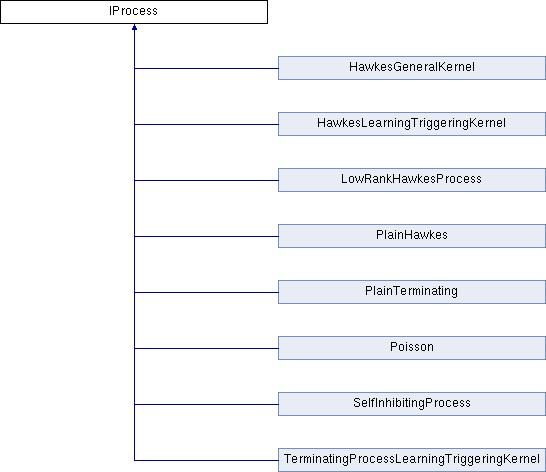
Implemented in PlainHawkes, TerminatingProcessLearningTriggeringKernel, HawkesLearningTriggeringKernel, PlainTerminating, HawkesGeneralKernel, LowRankHawkesProcess, SelfInhibitingProcess, and Poisson.
| virtual void IProcess::NegLoglikelihood |
( |
double & |
objvalue, |
|
|
Eigen::VectorXd & |
Gradient |
|
) |
| |
|
pure virtual |
Returns the negative loglikelihood value and the gradient vectors. Given a collection of sequences \(\mathcal{C} = \{\mathcal{S}^c\}\) where \(\mathcal{S}^c = \{t^{c,d}_i\}^{d=1\dotso D}_{i=1\dotso n^c_d}\), and \(n^c_d\) is the number of events on dimension d in sequence \(\mathcal{S}^c\). The negative loglihood of observing \(\mathcal{C}\) is defined as
\begin{align} \ell(\mathcal{C}) = - \sum_{d=1}^D\frac{1}{|\mathcal{C}|}\sum_{c=1}^{|\mathcal{C}|}\Bigg(\sum_{i=1}^{n^c_d}\lambda^*_d(t_i^{c,d}) - \int_{0}^{T_c}\lambda^*_d(\tau)d\tau\Bigg), \end{align}
where \(T_c\) is the observation window of the sequence \(\mathcal{S}^c\).
- Parameters
-
| [out] | objvalue | the objective function value, which is the negative log-likelihood value evaluated on the given set of sequences using the current model parameters. |
| [out] | Gradient | the gradient vector w.r.t. the model parameters. |
Implemented in PlainHawkes, TerminatingProcessLearningTriggeringKernel, HawkesLearningTriggeringKernel, HawkesGeneralKernel, PlainTerminating, LowRankHawkesProcess, SelfInhibitingProcess, and Poisson.
| virtual double IProcess::PredictNextEventTime |
( |
const Sequence & |
data, |
|
|
const unsigned & |
num_simulations |
|
) |
| |
|
pure virtual |
 1.8.11
1.8.11